Restricted choice?
#21

Posted 2009-September-20, 14:29
"Question from my daughter:
I have 3 children and one of them is a boy. What is the probability that they are all 3 boys?"
Since the question came from his daughter, I suggest that the probability that all three of his children are boys is zero.
But if we take it as a typical textbook question the answer is 1/7 as Elianna said and for the reasons that she said, and 1/(2^n-1) with n kids, as Helene said. Restricted choice involves an ongoing collection of information and some assumptions about who would do what. For example if your opponent always plays the J from QJ tight then the probability that he holds the Q when he drops the J is about 1/2 and the probability that he holds the J when he drops the Q is zero (which is why one should play the quacks randomly, but is an assumption in the analysis that your opponent does so). In the question as posed, it is very reasonable to interpret it as "We choose a family from among all families that have exactly 3 kids, at least one of whom is a boy, what is the probability that all 3 are boys?". You can jazz it up with biological and social data. For example, some parents wish to have at least one boy and at least one girl. To take that to extremes, suppose all parents quit producing after 1 child of each sex and always have a third child after having two of the same sex. Then, given that the family has three children one of them being a boy, the birth sequence must have been ggb, or bbb, or bbg. The probability that all three are boys is perhaps 1/3. But further, bbg and ggb would then remain 3 child families, while bbb would not. So you might need to ask the age of the youngest child. Of course not all parents make such choices, but some do and it will influence the percentages in the real world.
This assumes that you wish to take the problem as a truly practical problem. Surely the intended interpretation is the one that leads to the answer 1/7. Whether census data would agree with this figure I do not know. My guess is that it would not agree because of some of the points raised.
Here is a thought about restricted choice that I have never seen mentioned: Playing 5 card majors you open 1H, you eventually play 4H, You hold AKT32, dummy holds 7654. You win the opening side suit lead in your hand and you lay down the ace of hearts. LHO plays a quack. Restricted choice makes it 2 to 1 that the other quack is on your right? Not so fast. Holding Q9 it is (fairly) safe for lho to drop the Q. If partner has the K he still gets it, if declarer has the K defender was (probably) not getting your Q anyway. If defender can induce declarer to go to the board planning on making a restricted choice play this may use up a dummy entry when the suit was 2-2 all along. Defender won't get a trump trick but he wasn't going to get one anyway, and there may be a tactical advantage. At any rate, the 2 to 1 odds only really get set if declarer does go to the board, leads a spot, and RHO follows low. Now it is known that LHO held either QJ tight or a stiff. Now it is 2 to 1 for the well-known reasons. But when the Q first fell, I would say the evidence is not quite in.
Youu can vary the question of course.
#22

Posted 2009-September-20, 16:07
#23

Posted 2009-September-20, 17:57
EricK, on Sep 20 2009, 05:07 PM, said:
Since we are given the answer (1/7), it's clear they meant "at least one of the three children is a boy" because other interpretations of the question would result in different answers. :-) English is sloppy enough that I don't think there is some hard-and-fast way to interpret the original statement -- everybody could have a differing and equally valid view. :-)
Regarding the trump one... I imagine the implicit odds there depend greatly on the quality of the players. For fish like me, I might throw the Q of QJ but I'd never throw the Q in Q9 in that situation, even though the logic makes sense :-)
#24

Posted 2009-September-20, 18:06
blackshoe, on Sep 20 2009, 08:19 PM, said:
3for3, on Sep 20 2009, 01:10 PM, said:
<raises eyebrow>
You sure about that?
yep definitely sure, but then boys are dying much quicker so in the 70+ camp there are more women than men. I also have the feeling that subsequent children are more likely to be of the gender of the first child (this probably just means that a given couple have a predisposition to give birth to one gender, in fact I don't know how the two effects could be differentiated) but I never saw solid statistical proof for this, I tried googling it and found nothing.
George Carlin
#25

Posted 2009-September-20, 18:12
As for tv, screw it. You aren't missing anything. -- Ken Berg
Our ultimate goal on defense is to know by trick two or three everyone's hand at the table. -- Mike777
I have come to realise it is futile to expect or hope a regular club game will be run in accordance with the laws. -- Jillybean
#26

Posted 2009-September-20, 18:15
As for tv, screw it. You aren't missing anything. -- Ken Berg
Our ultimate goal on defense is to know by trick two or three everyone's hand at the table. -- Mike777
I have come to realise it is futile to expect or hope a regular club game will be run in accordance with the laws. -- Jillybean
#27

Posted 2009-September-20, 18:33
George Carlin
#28

Posted 2009-September-20, 20:25
EricK, on Sep 20 2009, 05:07 PM, said:
Upon reflection, I guess I agree. The statement focuses on the parent having 3 children one of which is a boy, rather than on the boy, so I think that indicates a randomly chosen family (or parent, which is the same thing) but I concede that it is not exactly an unchallengeable interpretation.
As to zero:
I was of course joking a bit about the probability being zero because his daughter asked him, and stretching a bit to make the father the referent of the pronoun I. There are no quotes around the statement so I figured I could argue the point, but w/o serious intent.
Moral of the story: Probability problems very often come down to describing precisely what is being analyzed. Deterministic problems often (but not always) are forgiving of vague formulations. Probability problems are ruthless.
#29

Posted 2009-September-21, 01:03
kenberg, on Sep 21 2009, 02:25 AM, said:
This was really my point. The fact that they gave the answer of 1/7 means they had a certain interpretation in mind. However the fact that they didn't make all the assumptions clear in the problem means that there is a fair chance they don't understand what assumptions underlie their answer and why they are important.
And that is worrying if this question came from someone trying to teach probability.
#30

Posted 2009-September-21, 03:09
helene_t, on Sep 20 2009, 07:11 PM, said:
I agree but I fail to see where is the other appraoch failing.
#31

Posted 2009-September-21, 03:29
Like the non black non raven paradox, it depends if you were looking for a random non black thing that turned out to be a non raven OR a random non raven that turned out not to be black. These delimitations sound a little ridiculous to me. Well maybe the paradox was also a little ridiculous.
George Carlin
#32

Posted 2009-September-21, 07:11
EricK, on Sep 21 2009, 02:03 AM, said:
kenberg, on Sep 21 2009, 02:25 AM, said:
This was really my point. The fact that they gave the answer of 1/7 means they had a certain interpretation in mind. However the fact that they didn't make all the assumptions clear in the problem means that there is a fair chance they don't understand what assumptions underlie their answer and why they are important.
And that is worrying if this question came from someone trying to teach probability.
It may be a thread hijack to go far into this but I see this as an instance of a fairly major problem, especially in regard to standardized tests. Far too often, the questions are vaguely phrased but students are expected to interpret them in a specific manner. If a student wants to do well, it is best that he not think deeply about the question. Rewarding superficial thought and punishing reflective questioning is presumably not the intent of the exams but I think that it often comes to that. Back in my school days, my fundamental rule for multiple choice exams was to never give any serious thought to any question. This strategy worked well.
#33

Posted 2009-September-21, 09:14
Parents with three daughters try once more
and then it's fifty-fifty they'll have four.
But those with a son or sons will let things be.
Hence all these surplus women, QED.
Actually someone told me that the relative birthrate depends on a number of external factors such as wars, diet, diets resulting from wars etc. I don't know if that is apocryphal
Psyche (pron. sahy-kee): The human soul, spirit or mind (derived, personification thereof, beloved of Eros, Greek myth).
Masterminding (pron. m
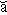 s
s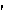 t
t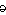 r-m
r-m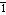 nd
nd ing) tr. v. - Any bid made by bridge player with which partner disagrees.
ing) tr. v. - Any bid made by bridge player with which partner disagrees."Gentlemen, when the barrage lifts." 9th battalion, King's own Yorkshire light infantry,
2000 years earlier: "morituri te salutant"
"I will be with you, whatever". Blair to Bush, precursor to invasion of Iraq
#34

Posted 2009-September-21, 09:21
1eyedjack, on Sep 21 2009, 04:14 PM, said:
Parents with three daughters try once more
and then it's fifty-fifty they'll have four.
But those with a son or sons will let things be.
Hence all these surplus women, QED.
I don't think that influences the sex ratio much.
By far the most important reason for the lack of male surplus is that boys are more likely to die than girls are.
#35

Posted 2009-September-21, 09:30
Fluffy, on Sep 21 2009, 10:09 AM, said:
helene_t, on Sep 20 2009, 07:11 PM, said:
I agree but I fail to see where is the other appraoch failing.
Suppose that BGG means that the first kid whose sex you determine is a boy while the too later were girls; if it was the last kid to have its sex to determined that was a boy, you would write GGB.
Then the event that one of the three children is known to be a boy while the two others are yet to be decided, leaves only four possible combinations:
BBB
BBG
BGB
BGG
So you have to distinguish between these two scenarios:
1) Only one child had its sex determined and it turned out to be a boy. The sex of the other two children have not been determined. In that case, the chance that all three are boys is 1/4.
2) The sex of all three children is known and at least one of them is a boy. In that case, the answer is 1/7.
If the information given is simply "at least one of the children is a boy" then there is no answer. You have to be more specific about what it is that you know.
#36

Posted 2009-September-21, 09:39
#37

Posted 2009-September-21, 09:42
As you may be aware, the jingle above draws the wrong conclusion. Put aside for the moment the fact that parents with 3 children of the same sex might in fact have a genetic predisposition for having children of that sex. Assume, as the jingle says, it is 50-50. Well, 50-50 is 50-50. If each pregnancy has a 50-50 chance of producing a girl then trying again with three daughters but letting it be with at least one boy will still mean that the pregnancy has a 50-50 chance of introducing another girl. Such a policy would influence the distribution of families with various configurations. For example, if followed strictly then there would be no families with three girls and two boys (unless the boys were twins) because by the time they had four children they would have had at least one boy and they would let it be. But influencing family configurations is not the same as influencing the overall percentage of girls.
Now if we introduce the possibility that having three girls is an indicator that the next pregnancy has a better than 50-50 chance of being a girl then yes, following this policy could increase the percentage of female births.
So: If you believe that families often keep at it until they have at least one boy then the fact that boys are more than 50% of the births would be some (weak) evidence against the idea that having three girls indicates a genetic predisposition for giving birth to girls.
#38

Posted 2009-September-21, 10:26
Fluffy, on Sep 21 2009, 04:39 PM, said:
Your numbers add up to 12 so it would be 3/12 which is correct.
#39

Posted 2009-September-21, 11:23
They are more likely to be involved in violent incidents.
They are more prone to various genetic disease (because they only have one X chromosome and where a girl might be able to compensate for a defective gene on one X chromosome with a normal gene on the other, a boy can't)
They are more prone to risk taking
They are genetically programmed to spend less resources on repairing the body and more resources on being vigorous in youth and middle age (essentially for the reasons above)
Because of this, although men outnumber women at birth, women end up outnumbering men in almost every age range.
Where a society has a surplus of men, it is always because of female infanticide (whether after birth, or via selective abortion)
#40

Posted 2009-September-21, 13:38
Dioxin pollution causes a more significant drop in the male birth rate. This has been observed in one Russian city and in some parts of SE Asia.
There's a small community in Canada where the male birth rate has gone from 52% in 1993 to 33% some years later. It is located near a large industrial area and the exact reason is unknown.

 Help
Help

