HCP Splits
#1

Posted 2013-September-28, 08:55
So far West has shown up with 9HCP and East 3HCP. Does this fact alone suggest playing East for the Q♦ (i.e. excluding any possible inferences from the bidding)?
Before today I would have thought that it was still a 50-50 chance but a bridge book I own suggests that in this situation you should play for the most even HCP split and therefore put East with the Q.
I appreciate that before the hand starts the HCP are likely to split evenly but I thought this wouldn't be the case a posteriori. The phrases "Bayes probability" and "Monty Hall" are floating around my head, but I am not a mathematician. Can someone help me on this point?
Thanks.
#2

Posted 2013-September-28, 09:59
For example, you say that the HCP are divided 9/3 and the ♦Q is not yet accounted for. If putting the ♦Q with the 9 HCP hand would have given that player a bid somewhere along the way, and he did not bid, then there is a reason for putting it in the other hand.
Otherwise, you are better off focusing on the distribution of suits rather than the distribution of HCP.
#3

Posted 2013-September-28, 10:06
Personally I distrust this analysis. Furthermore, we like to think of these scenarios as if there were no other information available, but that seldom is the case.
Psyche (pron. sahy-kee): The human soul, spirit or mind (derived, personification thereof, beloved of Eros, Greek myth).
Masterminding (pron. m
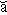 s
s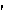 t
t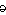 r-m
r-m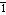 nd
nd ing) tr. v. - Any bid made by bridge player with which partner disagrees.
ing) tr. v. - Any bid made by bridge player with which partner disagrees."Gentlemen, when the barrage lifts." 9th battalion, King's own Yorkshire light infantry,
2000 years earlier: "morituri te salutant"
"I will be with you, whatever". Blair to Bush, precursor to invasion of Iraq
#4

Posted 2013-September-28, 10:42
 ArtK78, on 2013-September-28, 09:59, said:
ArtK78, on 2013-September-28, 09:59, said:
Thanks. I appreciate your point about inferences from the bidding but I am deliberately ignoring that aspect for now. Am I to take it from your answer that you think my book is wrong regarding HCP split?
 1eyedjack, on 2013-September-28, 10:06, said:
1eyedjack, on 2013-September-28, 10:06, said:
Furthermore, we like to think of these scenarios as if there were no other information available, but that seldom is the case.
Yes, I understand that I am couching the question in what might perhaps seem like an unrealistic scenario but I am just trying to sort out this particular issue in my head.
Another example for you - simpler (and with no vacant spaces implications), but I think it is much the same and it is troubling me. This time you are playing a contract and there are 2 aces unaccounted for. My book seems to suggest that upon finding one Ace with RHO you should place the other Ace with LHO because they are more likely to be split between the two defenders. I don't think this follows - sure at the beginning of the hand split aces was the most likely scenario but does that still hold true after discovering the position of one of the aces?
Hopefully this clarifies the question in my original post.
#5

Posted 2013-September-28, 12:22
#6

Posted 2013-September-28, 12:52
This post has been edited by Endymion77: 2013-September-29, 05:11
#7

Posted 2013-September-28, 14:00
The author started with the perfectly reasonable "when you are missing two aces, the chances are the same defender won't have both" and then drew these erroneous conclusions from that. I was sure I'd missed something.
#8

Posted 2013-September-29, 03:57
I can't help thinking that there must be something analogous to the theory of vacant spaces: the theory of vacant points, or vacant values. When there are 15 points missing, and one hand has shown up with 8 and the other nothing, and neither hand bid, then there are 3 vacant points in one hand A, and 11 in the other hand B, with 7 points to be distributed. Hand B is more likely to have the next missing points in the ratio of 11:3. ?
Endymion's argument of equal likelihood when there are 2 aces missing because there are only 4 initial possibilities is only valid if each of the 4 possibilities is equally likely. Once you assign different probabilities for those 4, then the conclusion is different.
In the extreme case, where hand A has shown 8 points and failed to open, but B has shown one ace, then I think Endymion might accept that A will not have the other ace. He therefore probably assigns a step function to the distribution of high card values, flat likelihood all the way to a sudden impossibility. I would think a more gradual transition of probabilities might apply.
Certainly if you are playing 7NT undoubled with 2 aces missing, and the person on lead shows up with one of them, I think it is fair to assume his partner has the other. Yes, we did have a case of someone being in 7NT undoubled minus one ace, and the leader eventually turned up with the ace. When asked why he didn't double, he said "Well, it was against you (respected senior player he was in awe of) and I thought you'd make it".
#9

Posted 2013-September-29, 04:25
#11

Posted 2013-September-29, 04:44
P1 P2
-----
A1 A2
x1 x2
A1 A2
x2 x1
A1 x1
A2 x2
A1 x1
x2 A2
A1 x2
A2 x1
A1 x2
x1 A2
A2 A1
x1 x2
A2 A1
x2 x1
A2 x1
A1 x2
A2 x1
x2 A2
A2 x2
A1 x1
A2 x2
x1 A1
x1 A1
A2 x2
x1 A1
x2 A2
x1 A2
A1 x2
x1 A2
x2 A1
x1 x2
A1 A2
x1 x2
A2 A1
x2 A1
x1 A2
x2 A1
A2 x1
x2 A2
x1 A1
x2 A2
A1 x1
x2 x1
A1 A2
x2 x1
A2 A1
In 12 of those cases, A1 is dealt to the first player (the one who showed up with the ace). However, once he shows with the ace, 8 times his other card is x1 or x2 and only 4 times his other card is A2. So it's more likely that the ace is in the other player.
The distributions I listed above:
Opp 1 - Opp 2
x - A1 A2
A1 - A2
A2 - A1
A1 A2 - x
aren't equally likely. Here's how often they happen:
Case 1: 4 times
Case 2: 8 times
Case 3: 8 times
Case 4: 4 times
Once it's between case 2 or case 4, case 2 is twice as likely (in the case of 4 cards only of course, when 13 cards are dealt the difference will be much more subtle but would still be there). So I hope I didn't confuse anyone.
#12

Posted 2013-September-29, 06:12
 helene_t, on 2013-September-29, 04:25, said:
helene_t, on 2013-September-29, 04:25, said:
That's right Helene. There are certainly a few errors it seems but a thoroughly enjoyable read.
 Endymion77, on 2013-September-29, 04:44, said:
Endymion77, on 2013-September-29, 04:44, said:
In 12 of those cases, A1 is dealt to the first player (the one who showed up with the ace). However, once he shows with the ace, 8 times his other card is x1 or x2 and only 4 times his other card is A2. So it's more likely that the ace is in the other player.
It's this point that reminded me of the Monty Hall problem, and exactly the point I was trying to understand - thanks for doing the analysis Endymion. On the face of it, it seems that the remaining ace is just as likely to be in either hand but I suppose the starting probabilities are still valid. I guess this analysis can be extended to HCP split as well as in my first example. But as others say above often there will be a known side suit to take into account.
#13

Posted 2013-September-29, 13:33
Nothing to do with the monty hall problem, though. That would entail a defender showing you a missing K and saying "still fancy the finesse?"
#14

Posted 2013-September-29, 16:05
That should make it clear that the vacant points argument is specious, without using information that would take into account the presence of the cards.
Added:
The other thing here is that the likelihood of the result depends on how many tricks have been played. At trick 13, the missing card is certain to turn up in the other hand. At trick 12 it is 2-1 to be in the other hand unless it would be limited by distribution at that point.
#15

Posted 2013-September-29, 17:33
Suppose lho shows up with 9 points more or less right away. Perhaps he starts wit the AKQ of clubs and you ruff the third round. Suppose it seems right to draw trump right away, you are missing the Q of trump, and there is another K out there somewhere, not in trump. Say it seems right to draw trump right way. OK, lho probably cannot have both the trump Q and the unseen K. Certainly he cannot have it if he was dealer, since he would have opened the bidding. So he can have the K w/o the Q, the Q w/o the K, or neither. All equally likely so the odds are 2 to 1 the Q is with rho.
That reasoning seems sound.
But if you have time to first locate the K with rho then, as near as I can see, we are back to 50-50.
Perhaps it makes sense to simply follow the advice of playing for the Q to be in the weaker hand. If it's 50-50, well, it's 50-50. And sometimes there will be an analysis, if you think long enough, to make it better than 50-50 that the Q LIES WITH rho. It would be unusual for lho to show up with 9 and for an analysis to show the Q is still more, rather than equally, likely to be with him. A corollary would be that after lho shows 9 points and you get the lead, you may as well play for the Q to be with rho w/o bothering to find the location of the missing K. If the K lies with lho then it is somewhere between highly likely and certain that the Q lies with rho. If the K lies with rho it's a coin flip. So just play rho for the Q.
#16

Posted 2013-September-30, 03:18
 Endymion77, on 2013-September-29, 04:44, said:
Endymion77, on 2013-September-29, 04:44, said:
Yes if you only give 2 cards to each player then the empty spaces argument would be strong. You can make it even stronger by giving just one card to each player - now knowing that LHO has one of the cards makes it a 100% bet that RHO has the other card!
But you give 13 cards to each player. Knowing that LHO has one of the aces makes it 12/25 that he also has the other ace.
In practice you will always know a lot more of course. But the OP's question was about the hypothetical situation that all we know is that LHO has ♠A. And the the question: what is the probability that LHO also has ♥A?
#17

Posted 2013-September-30, 04:19
 helene_t, on 2013-September-30, 03:18, said:
helene_t, on 2013-September-30, 03:18, said:
Yes, as I mentioned above "Once it's between case 2 or case 4, case 2 is twice as likely (in the case of 4 cards only of course, when 13 cards are dealt the difference will be much more subtle but would still be there)."
The number of unknown cards obviously depends on which trick the situation arises, it might easily happen when there are only 4 cards left in the defenders, or 6, or 26 (if it happens at trick 1).
 helene_t, on 2013-September-30, 03:18, said:
helene_t, on 2013-September-30, 03:18, said:
And the answer is that it depends on the number of remaining cards in the opponents but RHO is always more likely to have it.
#18

Posted 2013-September-30, 04:30
xx
opposite
KJx.
They suggest making a discovery play to see who has the ace in a different suit. Now if the player you finesse against had the ace in the other suit, you play him for the queen (by playing low to the Jack). Otherwise, you play him for the Ace (by playing low to the Ace).
This is clearly wrong since even if there is an empty space argument giving the player you finesse against an above-50% chance of holding the ace, the same would apply to the queen.
#20

Posted 2013-September-30, 05:06
 Endymion77, on 2013-September-29, 04:44, said:
Endymion77, on 2013-September-29, 04:44, said:
But surely in this four (relevant) card ending which you describe once RHO (say) has shown up with A1 LHO will have shown up with either x1 or x2 and so we are back to 50:50. So from what I can see this argument would only be relevant mid-trick which isn't of much use at all.
 fromageGB, on 2013-September-29, 13:33, said:
fromageGB, on 2013-September-29, 13:33, said:
I suppose what reminded me of Monty Hall was that you start off with a statement "it's unlikely both aces are in the same hand" and when one Monty/your opps reveal the position of one of the aces, does the original probability still apply like in Monty Hall. (Again let me stress I am not a mathematician.)
 Endymion77, on 2013-September-30, 04:19, said:
Endymion77, on 2013-September-30, 04:19, said:
Again doesn't this only follow if you haven't seen the other opp follow with a small x?
 helene_t, on 2013-September-30, 04:30, said:
helene_t, on 2013-September-30, 04:30, said:
xx
opposite
KJx.
For completeness' sake I may as well post the whole problem as I think the authors have made not only a maths error but a bridge error too.
So as Helene says the author suggests that an expert would locate the A♣ before playing on diamonds, playing whoever showed up with the ♣A not to also have the ♦A - apparently fallacious logic as discussed above. However it looks to me like the hand should be played by ruffing out spades, drawing trumps and playing to the JD endplaying East if he wins with the Q.

 Help
Help

